밑바닥부터 시작하는 비트코인

티스토리 뷰

블록체인/Bitcoin

밑바닥부터 시작하는 비트코인 - 2장 타원곡선

piatoss 2023. 8. 27. 13:35

본 게시글에서는 저서 '밑바닥부터 시작하는 비트코인'의 Python으로 작성된 예제 코드를 Go로 컨버팅 하여 작성하였습니다.

📺 시리즈

2023.08.25 - [블록체인/비트코인] - 밑바닥부터 시작하는 비트코인 - 1장 유한체

🐱‍👤 전체 코드

GitHub - piatoss3612/bitcoin-from-scratch

Contribute to piatoss3612/bitcoin-from-scratch development by creating an account on GitHub.

github.com

📕 타원곡선 정의

타원곡선은 다음과 같은 식으로 나타냅니다.

y² = x³ + ax + b

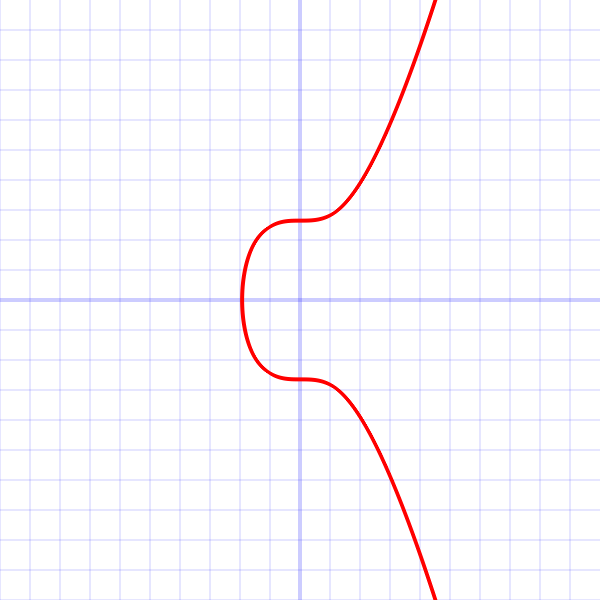
위의 방정식을 그래프로 표현하면 아래와 같습니다.

출처: https://medium.com/coinmonks/learn-how-to-code-elliptic-curve-cryptography-a952dfdc20ab

y² 항으로 인해 그래프가 x축 대칭되는데, 3차 방정식 그래프를 y > 0인 부분에 대해 곡선을 완만하게 하여 x축 대칭이 되도록 만든 그래프로 생각할 수 있습니다.

비트코인에서 사용되는 타원곡선은 secp256k1이라고 하며 다음과 같은 식으로 나타냅니다.

y² = x³ + 7

출처: https://en.bitcoin.it/wiki/Secp256k1

💻 Go로 타원곡선 코딩하기

곡선 자체보다는 곡선 위의 개별 점들에 초점을 맞추고 진행합니다.

// 타원곡선의 점을 나타내는 구조체
type Point struct {
	x, y, a, b int
}

// 타원곡선의 점을 생성하는 함수
func New(x, y, a, b int) (*Point, error) {
	// 주어진 점이 타원곡선 위에 있는지 확인
	if y*y != x*x*x+a*x+b {
		return nil, fmt.Errorf("(%d, %d) is not on the curve", x, y)
	}

	return &Point{x: x, y: y, a: a, b: b}, nil
}

// 타원곡선의 점을 문자열로 표현하는 함수 (Stringer 인터페이스 구현)
func (p Point) String() string {
	return fmt.Sprintf("Point(%d, %d)_%d_%d", p.x, p.y, p.a, p.b)
}

// 두 타원곡선의 점이 같은지 확인하는 함수
func (p Point) Equals(other Point) bool {
	// 두 점의 좌표가 같고 같은 타원곡선 위에 있는지 확인
	return p.x == other.x && p.y == other.y &&
		p.a == other.a && p.b == other.b
}

// 두 타원곡선의 점이 다른지 확인하는 함수
func (p Point) NotEquals(other Point) bool {
	return !(p.x == other.x && p.y == other.y &&
		p.a == other.a && p.b == other.b)
}

Python 예제와의 차이점

구조체를 사용했습니다.
생성자 함수를 추가했습니다.
연산자 오버로딩이 불가능한 대신 구조체의 메서드로 기능을 구현했습니다.

➕ 두 점의 덧셈

타원곡선과 직선의 관계

~~직선이 타원곡선 위의 한 점을 지나는 경우~~
직선이 타원곡선 위의 세 점을 지나는 경우
직선이 y축과 평행한 경우
직선이 타원곡선의 한 점에 접하는 접선인 경우

타원곡선에서 점 덧셈의 정의

두 점 P와 Q를 지나는 직선이 타원곡선과 만나는 교점을 x축으로 대칭시킨 점을 P+Q로 정의합니다.
(직선이 타원곡선 위의 한 점을 지나는 경우는 덧셈을 정의할 수 없습니다.)

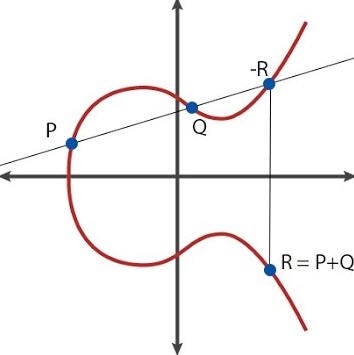
타원곡선의 점 덧셈은 비선형 연산으로, 결과를 쉽게 예측할 수 없다는 성질을 가지고 있습니다.

🧫 점 덧셈 성질

점 덧셈은 일반 덧셈 연산과 유사한 몇 가지 성질을 만족합니다.

1. 항등원, 역원 존재

곡선 위의 점 A와 더한 결과가 A가 되는 곡선 위의 점 I가 존재합니다. 이 점을 무한원점(point at infinity)이라고 합니다.

곡선 위의 점 A에 대해 덧셈의 역원 -A가 존재하고, 그 합은 항등원인 I가 됩니다.

I + A = A
A + (-A) = I

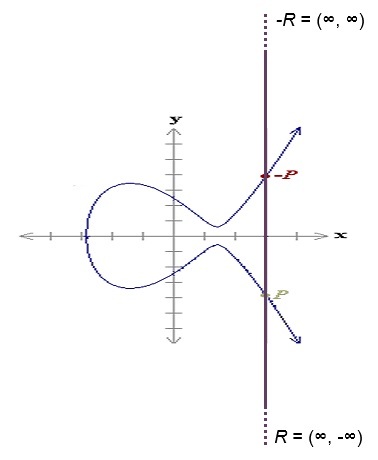
출처: https://www.herongyang.com/EC-Cryptography/Introduction-Infinity-Point-on-Elliptic-Curve.html

x축과 수직인 직선과 타원곡선이 만나는 두 점의 덧셈으로 세 번째 점인 무한원점을 구할 수 있고, 무한원점은 실제로 존재하는 점이라기 보다는 무한대에 있다고 상상(?)할 수 있습니다.

2. 교환법칙

A와 B를 지나는 직선은 순서를 바꿔도 동일한 위치에서 곡선과 만납니다.

A + B = B + A

3. 결합법칙

3개 이상의 덧셈에서 어느 두 항을 먼저 더하더라도 결과는 동일합니다.

(A + B) + C = A + (B + C)

💻 점 덧셈 코딩하기

x축에 수직인 직선 위의 두 점을 먼저 다룹니다.

// 타원곡선의 점을 생성하는 함수
func New(x, y, a, b int) (*Point, error) {
	// 무한원점인지 확인
	if x == math.MaxInt64 && y == math.MaxInt64 {
		return &Point{x: x, y: y, a: a, b: b}, nil
	}

	// 주어진 점이 타원곡선 위에 있는지 확인
	if y*y != x*x*x+a*x+b {
		return nil, fmt.Errorf("(%d, %d) is not on the curve", x, y)
	}

	return &Point{x: x, y: y, a: a, b: b}, nil
}

// 타원곡선의 점을 문자열로 표현하는 함수 (Stringer 인터페이스 구현)
func (p Point) String() string {
	// 무한원점인지 확인
	if p.x == math.MaxInt64 && p.y == math.MaxInt64 {
		return "Point(infinity)"
	}
	return fmt.Sprintf("Point(%d, %d)_%d_%d", p.x, p.y, p.a, p.b)
}

// 두 타원곡선의 점을 더하는 함수
func (p Point) Add(other Point) (*Point, error) {
	// 같은 타원곡선 위에 있는지 확인
	if p.a != other.a || p.b != other.b {
		return nil, fmt.Errorf("points %s and %s are not on the same curve", p, other)
	}

	/* case1: 두 점이 x축에 수직인 직선 위에 있는 경우 */

	// p가 무한원점인지 확인
	if p.x == math.MaxInt64 && p.y == math.MaxInt64 {
		return &other, nil
	}

	// other가 무한원점인지 확인
	if other.x == math.MaxInt64 && other.y == math.MaxInt64 {
		return &p, nil
	}

	// 한 점에 그의 역원을 더하는 경우, 무한원점을 반환
	if p.x == other.x && p.y != other.y {
		return New(math.MaxInt64, math.MaxInt64, p.a, p.b)
	}

	// TODO: 이후에 구현
	return nil, nil
}

Python 예제와의 차이점

x와 y값이 math.MaxInt64인 경우, 무한원점으로 취급했습니다.

➕ x₁ ≠ x₂인 경우의 점 덧셈

서로 다른 두 점의 덧셈은 먼저 두 점을 지나는 직선의 기울기를 구해야 합니다. 기울기 s는 아래와 같이 구할 수 있습니다.

P₁ = (x₁, y₁), P₂ = (x₂, y₂), P₃ = (x₃, y₃)
P₁ + P₂ = P₃
s = (y₂ - y₁) / (x₂ - x₁)

기울기를 구하고 나면 P₃은 아래 공식으로 구할 수 있습니다. 여기서 P₃은 P₁과 P₂를 지나는 직선이 곡선과 만나는 세 번째 점을 y축으로 대칭한 점이라는 것을 기억해야 합니다.

x₃ = s² - x₁ - x₂
y₃ = s(x₁ - x₃) - y₁

점 덧셈 공식 유도

기울기: s = (y₂ - y₁) / (x₂ - x₁)

두 점을 지나는 직선: y = s(x - x₁) + y₁

타원곡선: x³ + ax + b

직선은 타원곡선과 세 점에서 만나므로 직선을 타원곡선에 대입하면 다음을 얻습니다.

y² = (s(x - x₁) + y₁)² = x³ + ax + b

모든 항을 미지수 x의 차수에 따라 한쪽으로 모아 내림차순으로 정리하면 다음을 얻습니다.

x³ - s²x² + (a + 2s²x₁ - 2sy₁)x + b -s²x₁² + 2sx₁y₂ - y₁² = 0

x₁, x₂, x₃는 이 방정식을 만족하는 근이므로 다음과 같이 나타낼 수 있습니다.

(x - x₁)(x - x₂)(x - x₃) = x³ - (x₁ + x₂ + x₃)x² + (x₁x₂ + x₁x₃ + x₂x₃)x - x₁x₂x₃ = 0

근이 같은 두 방정식에서 x의 같은 차수의 계수들은 서로 같아야 합니다. x²의 계수를 비교하여 다음을 얻습니다.

s² = x₁ + x₂ + x₃

x₃ = s² - x₁ - x₂

그리고 이렇게 구한 x₃을 직선에 대입하면 -y₃를 구할 수 있습니다. y₃를 구하기 위해 부호를 반대로 설정해 줘야 함에 주의합니다.

y₃ = s(x₁ - x₃) - y₁

➕ x₁ ≠ x₂인 경우의 점 덧셈 코딩하기

// 타원곡선의 점을 나타내는 구조체
type Point struct {
	x, y, a, b float64
}

// 타원곡선의 점을 생성하는 함수
func New(x, y, a, b float64) (*Point, error) {
	// 무한원점인지 확인
	if x == math.MaxFloat64 && y == math.MaxFloat64 {
		return &Point{x: x, y: y, a: a, b: b}, nil
	}

	// 주어진 점이 타원곡선 위에 있는지 확인
	if y*y != x*x*x+a*x+b {
		return nil, fmt.Errorf("(%.2f, %.2f) is not on the curve", x, y)
	}

	return &Point{x: x, y: y, a: a, b: b}, nil
}

// 두 타원곡선의 점을 더하는 함수
func (p Point) Add(other Point) (*Point, error) {
	// 같은 타원곡선 위에 있는지 확인
	if p.a != other.a || p.b != other.b {
		return nil, fmt.Errorf("points %s and %s are not on the same curve", p, other)
	}

	/* case1: 두 점이 x축에 수직인 직선 위에 있는 경우 */

	// p가 무한원점인지 확인
	if p.x == math.MaxFloat64 && p.y == math.MaxFloat64 {
		return &other, nil
	}

	// other가 무한원점인지 확인
	if other.x == math.MaxFloat64 && other.y == math.MaxFloat64 {
		return &p, nil
	}

	// 한 점에 그의 역원을 더하는 경우, 무한원점을 반환
	if p.x == other.x && p.y != other.y {
		return New(math.MaxFloat64, math.MaxFloat64, p.a, p.b)
	}

	/* case2: 두 점이 같은 경우 */

	/* case3: 두 점이 서로 다른 경우 */

	// p와 other를 지나는 직선의 기울기 구하기
	s := (other.y - p.y) / (other.x - p.x)

	// p와 other를 지나는 직선이 타원곡선과 만나는 다른 한 점 q의 좌표 구하기
	nx := s*s - p.x - other.x
	ny := s*(nx-p.x) + p.y

	// p와 other의 점 덧셈의 결과인 q의 역원 구하기 (y축 대칭)
	ny = -ny

	return New(nx, ny, p.a, p.b)
}

변경점

구조체 필드의 타입을 int에서 float64로 변경했습니다.
무한원점을 확인하기 위한 값을 math.MaxInt64에서 math.MaxFloat64로 변경했습니다.

➕ P₁ = P₂인 경우의 점 덧셈

곡선 위의 동일한 두 점을 이은 직선은 그 점에서의 접선을 의미합니다. 따라서 동일한 두 점의 점 덧셈 결과를 구하기 위해 접선이 곡선과 만나는 다른 교점을 찾아야 합니다.

출처: https://www.herongyang.com/EC-Cryptography/Introduction-Same-Point-Addition-on-Elliptic-Curve.html

접선의 기울기 s는 아래와 같이 구할 수 있습니다.

s = (3x₁² + a) / (2y₁)

P₃을 구하는 공식은 x₁ = x₂라는 조건을 앞서 서로 다른 두 점을 더하기 위해 사용했던 공식에 대입하여 수 있습니다.

x₃ = s² - 2x₁
y₃ = s(x₁ - x₃) - y₁

접선의 기울기 유도

타원곡선을 미분하여 도함수를 구하면 접선의 기울기 공식을 구할 수 있습니다.

y² = x³ + ax + b

양변을 미분하면 다음을 얻습니다.

2y dy = (3x² + a) dx

dy / dx = (3x² + a) / (2y)

구한 기울기 공식에 x₁과 y₁을 대입하면 기울기 s를 구할 수 있습니다.

s = (3x₁² + a) / (2y₁)

💻 P₁ = P₂인 경우의 점 덧셈 코딩하기

// 두 타원곡선의 점을 더하는 함수
func (p Point) Add(other Point) (*Point, error) {
	...

	/* case2: 두 점이 같은 경우 */

	// p와 other가 같은 점인지 확인
	if p.x == other.x && p.y == other.y {
		// 접선의 기울기 구하기
		s := (3*p.x*p.x + p.a) / (2 * p.y)

		// 접선과 타원곡선의 교점 q의 좌표 구하기
		nx := s*s - 2*p.x
		ny := s*(nx-p.x) + p.y

		// 교점 q의 역원 구하기 (y축 대칭)
		ny = -ny

		return New(nx, ny, p.a, p.b)
	}

	...

	return New(nx, ny, p.a, p.b)
}

💻 마지막 예외 처리 코딩하기

접선이 x축에 수직인 경우 한 가지 예외 상황이 존재합니다. 두 점이 같으면서 y가 0인 경우에 분모가 0이 되어 기울기를 구할 수 없습니다. 이 경우에는 무한원점을 반환하도록 예외 처리를 해줍니다.

// 두 타원곡선의 점을 더하는 함수
func (p Point) Add(other Point) (*Point, error) {

	...

	/* case2: 두 점이 같은 경우 */

	// p와 other가 같은 점인지 확인
	if p.x == other.x && p.y == other.y {
		// 예외 처리: 접선이 x축에 수직인 경우 무한원점을 반환
		if p.y == 0 {
			return New(math.MaxFloat64, math.MaxFloat64, p.a, p.b)
		}
		// 접선의 기울기 구하기
		s := (3*p.x*p.x + p.a) / (2 * p.y)

		// 접선과 타원곡선의 교점 q의 좌표 구하기
		nx := s*s - 2*p.x
		ny := s*(nx-p.x) + p.y

		// 교점 q의 역원 구하기 (y축 대칭)
		ny = -ny

		return New(nx, ny, p.a, p.b)
	}

	...

	return New(nx, ny, p.a, p.b)
}

🎯 코드 리팩토링

package main

import (
	"fmt"
	"math"
)

// 타원곡선의 점을 나타내는 구조체
type Point struct {
	x, y, a, b float64
}

// 타원곡선의 점을 생성하는 함수
func New(x, y, a, b float64) (*Point, error) {
	// 무한원점인지 확인
	if isInfinity(x, y) {
		return &Point{x: x, y: y, a: a, b: b}, nil
	}

	// 주어진 점이 타원곡선 위에 있는지 확인
	if !isOnCurve(x, y, a, b) {
		return nil, fmt.Errorf("(%.2f, %.2f) is not on the curve", x, y)
	}

	return &Point{x: x, y: y, a: a, b: b}, nil
}

// 타원곡선의 점을 문자열로 표현하는 함수 (Stringer 인터페이스 구현)
func (p Point) String() string {
	// 무한원점인지 확인
	if isInfinity(p.x, p.y) {
		return "Point(infinity)"
	}
	return fmt.Sprintf("Point(%.2f, %.2f)_%.2f_%.2f", p.x, p.y, p.a, p.b)
}

// 두 타원곡선의 점이 같은지 확인하는 함수
func (p Point) Equals(other Point) bool {
	// 두 점의 좌표가 같고 같은 타원곡선 위에 있는지 확인
	return samePoint(p.x, p.y, other.x, other.y) &&
		sameCurve(p.a, p.b, other.a, other.b)
}

// 두 타원곡선의 점이 다른지 확인하는 함수
func (p Point) NotEquals(other Point) bool {
	return !(samePoint(p.x, p.y, other.x, other.y) &&
		sameCurve(p.a, p.b, other.a, other.b))
}

// 두 타원곡선의 점을 더하는 함수
func (p Point) Add(other Point) (*Point, error) {
	// 같은 타원곡선 위에 있는지 확인
	if !sameCurve(p.a, p.b, other.a, other.b) {
		return nil, fmt.Errorf("points %s and %s are not on the same curve", p, other)
	}

	/* case1: 두 점이 x축에 수직인 직선 위에 있는 경우 */

	// p가 무한원점인지 확인
	if isInfinity(p.x, p.y) {
		return &other, nil
	}

	// other가 무한원점인지 확인
	if isInfinity(other.x, other.y) {
		return &p, nil
	}

	// 한 점에 그의 역원을 더하는 경우, 무한원점을 반환
	if areInverse(p.x, other.x, p.y, other.y) {
		return New(math.MaxFloat64, math.MaxFloat64, p.a, p.b)
	}

	/* case2: 두 점이 같은 경우 */

	// p와 other가 같은 점인지 확인
	if samePoint(p.x, p.y, other.x, other.y) {
		// case 2-1 예외 처리: 접선이 x축에 수직인 경우, 무한원점을 반환
		if p.y == 0 {
			return New(math.MaxFloat64, math.MaxFloat64, p.a, p.b)
		}
		// 접선의 기울기 구하기
		s := (3*p.x*p.x + p.a) / (2 * p.y)

		// 접선과 타원곡선의 교점 q의 좌표 구하기
		nx := s*s - 2*p.x
		ny := s*(nx-p.x) + p.y

		// 교점 q의 역원 구하기 (y축 대칭)
		ny = -ny

		return New(nx, ny, p.a, p.b)
	}

	/* case3: 두 점이 서로 다른 경우 */

	// p와 other를 지나는 직선의 기울기 구하기
	s := (other.y - p.y) / (other.x - p.x)

	// p와 other를 지나는 직선이 타원곡선과 만나는 다른 한 점 q의 좌표 구하기
	nx := s*s - p.x - other.x
	ny := s*(nx-p.x) + p.y

	// p와 other의 점 덧셈의 결과인 q의 역원 구하기 (y축 대칭)
	ny = -ny

	return New(nx, ny, p.a, p.b)
}

// 무한원점인지 확인하는 함수
func isInfinity(x, y float64) bool {
	return x == math.MaxFloat64 && y == math.MaxFloat64
}

// 타원곡선 위에 있는지 확인하는 함수
func isOnCurve(x, y, a, b float64) bool {
	return y*y == x*x*x+a*x+b
}

// 두 점이 서로 역원인지 확인하는 함수
func areInverse(x1, x2, y1, y2 float64) bool {
	return x1 == x2 && y1 != y2
}

// 두 타원곡선이 같은지 확인하는 함수
func sameCurve(a1, b1, a2, b2 float64) bool {
	return a1 == a2 && b1 == b2
}

// 두 점이 같은지 확인하는 함수
func samePoint(x1, y1, x2, y2 float64) bool {
	return x1 == x2 && y1 == y2
}

변경점

반복되어 사용되는 코드를 별도의 함수로 정의했습니다.

💯 테스트 결과

$ go test -v -cover .
=== RUN   Test_New
--- PASS: Test_New (0.00s)
=== RUN   Test_String
--- PASS: Test_String (0.00s)
=== RUN   Test_Equals
--- PASS: Test_Equals (0.00s)
=== RUN   Test_NotEquals
--- PASS: Test_NotEquals (0.00s)
=== RUN   Test_Add
--- PASS: Test_Add (0.00s)
=== RUN   Test_main
--- PASS: Test_main (0.00s)
PASS
coverage: 100.0% of statements
ok      elliptic-curve  0.002s  coverage: 100.0% of statements

📖 참고자료

밑바닥부터 시작하는 비트코인

비트코인은 블록체인 기술의 집약체입니다. 이더리움, 이오스 같은 2, 3세대 블록체인은 비트코인을 바탕으로 확장, 발전한 개념입니다. 디앱 개발에서 머무르지 않고 블록체인 개발자로 성장하

www.hanbit.co.kr

GitHub - jimmysong/programmingbitcoin: Repository for the book

Repository for the book. Contribute to jimmysong/programmingbitcoin development by creating an account on GitHub.

github.com

Learn how to code elliptic curve cryptography

This article gives an introduction to understanding elliptic curve cryptography and coding it.

medium.com

글에서 수정이 필요한 부분이나 설명이 부족한 부분이 있다면 댓글로 남겨주세요!

'블록체인 > Bitcoin' 카테고리의 다른 글

밑바닥부터 시작하는 비트코인 - 6장 스크립트 (0)	2023.09.11
밑바닥부터 시작하는 비트코인 - 5장 트랜잭션 (0)	2023.09.05
밑바닥부터 시작하는 비트코인 - 4장 직렬화 (0)	2023.09.02
밑바닥부터 시작하는 비트코인 - 3장 타원곡선 암호 (0)	2023.08.30
밑바닥부터 시작하는 비트코인 - 1장 유한체 (0)	2023.08.25

최근에 올라온 글

최근에 달린 댓글

« 2025/01 »
일	월	화	수	목	금	토
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

Total

Today

Yesterday

글 보관함

TAG more

개발 코어 강화 일지

티스토리 뷰